PGボックスとは
筆者(Takunoji Java※ツイッターへのリンクです)が学習した内容とJavaの学習方法などをアップしているブログです。主にGithubとYoutubeを使用して上記の内容を解説したり、忘備録として使用していました。しかし、いろいろ書いたものが、まとまっていないので、カテゴリごとにまとめました。
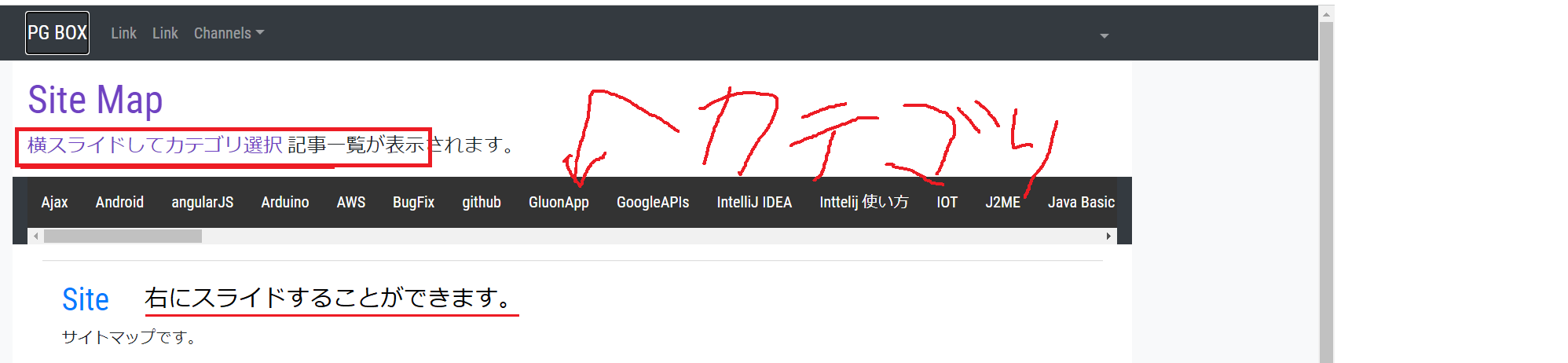
カテゴリについて
作成した記事はカテゴリごとに分けております。
こちらのページでは、カテゴリを選択することで、対象の記事一覧を下部(「Siteマップです」と書いてある部分)に表示します。※ちなみにAngular(JSのフレームワーク)を使用して作成しました。
並び替えは、新しいものから順になっているので、各カテゴリを選択すると作成した記事が初めから順番に表示されます。
おすすめとしては、次のカテゴリがちゃんと書けているのではなかろうか?と思っています。
- IntelliJ IDEA
- Inttelij 使い方
- Java Basic
- Java Basic Lv1
- Java Basic Lv2
- Java Basic Lv3
- Java はじめてから基本文法
- Java ワンポイント
- JavaBugFix
- JavaFX
- Javaチュートリアル(OracleDoc)
- Javaプログラム基礎
- JSワンポイント
- LWJGL Gitbook Chapter
他にもありますが、とりあえず。。。
下のページの使い方です。