イントロダクション
今まで、人工知能を理解したいと思色々と学習しましたが、どれも理解に至らず。。。
悩んだ挙句にたどり着いたのが、学習モデルを理解するというのがキーポイントになると思うに至りました。
では「学習モデルとは?」と悩んでいるとひょんなところに下のような本がありました。
|
|
早速学習開始です。本の内容は以下の通りです。
- 数理モデルとは
- データ分析と数理モデル
- 数理モデルの構成要素・種類
- 基礎的な数理モデル
- 少数の微分方程式によるモデル
- 確率モデル
- 統計モデル
- 高度な数理モデル
- 時系列モデル
- 機械学習モデル
- 強化学習モデル
- タ体系モデル・エージョントベースモデル
- 数理モデルを作る
- モデルを決めるための要素
- モデルを設計する
- パラメータを推定する
- モデルを評価する
以上のような内容でこの本は記述されています。
※目次を参照しました。
Javaで数学的なことをやろうとしたときに使えるのがND4Jです。これに関してはこちらの記事にインストール方法などを記載しています。
ちなみに、今まで学習したものに関しては下のリンクです。カテゴリ分けしているので「数理モデルとJava」というカテゴリで検索した結果です。
数学への挑戦履歴
数理モデルの理解
3度目の正直、今度こそ数理モデルを理解して「学習モデルの理解」につなげたいところです。
今までに調べたことでわかっていることは以下の部分です。
- 数理モデルの作り方を理解すれば、学習モデルも理解できそうだ。
- 色んな本でロジスティック回帰とか、マルコフ過程とかあるが、そこら辺はTensorFlowなどのフレームワークライブラリのメソッドで定義されているので入力と出力を理解すればよい(全部は見ていません)
たいしたことではないですが、「数理モデル」を理解できればあとは、プログラミングの知識(技術)で何とかなりそうだと思いました。
注意事項
「システム」という言葉がアプリケーション・システムと何かしらのデータを生成するものと二つの意味を持っているので注意してください。記載する内容に関しては「アプリケーション」と「データを生成するもの」のように書き分けています。
データを分析するということ
普段から我々は、いろんな情報をもとに世の中を理解・制御しています。
しかし、単純なことは問題なく理解と制御ができますが、複雑なことになるとそうもいきません。
なので以下の方法でそれを解決しようという試みです。
- 理解したいもの事の情報(データ)を観測などをして取得する
- そのデータを分析する
- 分析の結果からそのメカニズム・ルールを客観的に理解する
対象をデータ生成システムとして見る
データの生成システムと書かれてもよくわかりませんでしたが、このシステムを観測することでデータを取得(生成)できるので「データ生成システム」というわけなのですね。。。
システムとデータが下のようなものです。
システム
- A.生物現象
- B.物理現象
- C.社会現象
- D.顧客の行動
データ
- A -> イナゴの大量発生
- B -> 交通渋滞
- C -> 少子高齢化社会
- D -> 売れ筋商品の予想
そして、これらの関係は下のようなものです。
システムを観測するとデータが取得できる
データを調べ、データの生成ルールを推測できる(できないものもある)
データ分析のアプローチ
アプローチその1: 要素還元
- 分類可能な少ない種類の要素の集まりとして理解
ある物事(システム) -> 要素分解 -> 理解 -> 応用・制御
例:※とてもシンプルにしています。
システム=自転車に乗るための技術
要素={ バランスを取る, ペダルをこぐ}
理解1=自転車に乗ってバランスをとる練習をする
理解2=自転車に乗ってペダルをこぐ
応用・制御=自転車に乗れるようになる
アプローチその2: 深層学習(Deep Leaning)
- 複雑なものは複雑なまま理解
この様な物事に関して理解をするためには「数理モデル」を使用して、以下の課題を解決する
- 現象のメカニズムを客観的な方法で明らかにする
- データから未来を予測する
- コンピュータに高度なデータ処理・データ生成をやらせる
そして、数理モデルとは?に対する答えは下のような記述がありました。
数理モデルとは数学的な手段を用いて記述された、対象のデータ生成ルールを模したもの
つまり疑似データ生成ルールということです。
数理モデルの役割
平均値、標準偏差などを算出してその結果を眺めて対象データを分析することも立派な分析ですが、
・現象のメカニズムを客観的な方法で明らかにする
・データから未来を予測する
・コンピュータに高度なデータ処理、データ生成をやらせる
などのように、眺めても分析できないことがあるので、それを解決します。
数理モデルは仮定である
推理小説に出てくるような「仮定」をたてて、それを使用して対象になるシステム(データを生成するもの事)と同じようなデータを出してくれるように調整します。
手順としては以下の通りです。
- 「仮定(数理モデル)」をたてる(つくる)
- 対象システムと同じようなデータを生成するように調整する
- できた数理モデルが、どれだけ対象(システム)を表現できているか検証する
つまりは、仮定がどれだけ現象のメカニズムに近いのか?ここが重要になり、数理モデルによって得られたデータが現実に近ければ近いほど数理モデルは生き生きと振る舞いを見せるということらしいです。
※本を読んで理解したところなので「らしい」と記載しています。
数理モデルの構成要素
- 変数
- 数理構造
- パラメータ
1.変数:変数で表す
数理モデルを作るための初めに一歩は「変数を作ること」です。
変数とは、対象となるシステムの「状態」「性質」「量」などを数字やラベルで表したもの
変数は3種類
-
値の性質による分類
-
- 量的変数:たし算、引き算ができる変数のこと
- (Ex)
- 体重・身長など=人の特徴を示すときに使用する
-
- 質的変数:行ってよい操作・ダメな操作を判別する場合に使用する
- (Ex)
- 性別・趣味・テストの順位など、またの名をカテゴリ変数
-
-
観測できるかどうかによる分類
-
- 観測変数:直接観測(測定)可能な変数
- (Ex)
- ある顧客がコンビニで商品を購入したとき、「何をいくつ買ったのか?」
-
- 潜在変数:直接観測(測定)できない変数
- (Ex)
- ある顧客がコンビニで商品を購入したとき、「なぜその商品を買ったのか?」
- 説明する/されるかによる分類
-
- 目的変数:原因を受けて発生した結果を示す変数
- (Ex)
- バネに重りをつけ、バネの伸び率を見た場合には「原因にあたる『重りの重さ』」が目的変数になる
-
- 説明変数:何かの原因となっている変数
- (Ex)
- バネに重りをつけ、バネの伸び率を見た場合には「原因にあたる『重りの重さ』」が説明変数になる
-
-
2. 数理構造=数理モデルの骨組
下のような説明がありました。はっきりとはしませんが、今後出てくる「方程式」や「アルゴリズム」のことと理解しています。※ニュートンの運動方程式、マクスウェルの方程式など。。。
数学的に表現する時に必要な数式、適切な数理構造を選ぶことが良い分析のかなめになります。
3. パラメータ=数理モデルを動かすもの
数理モデルの振る舞いをデータに沿わせるための「稼働域」を制御するもの
モデルをデータに合わせる「フィッティング」を行うことで数理モデルが完成します。
パラメータは、数が多くなると「可動領域が多く」なりますので、パラメータの数は適切な数にする必要がある。
このパラメータに関しては、学習を進めていく中で理解する必要があるみたいです。
微分は「何かの、何かに対する変化の割合を計算したもの」
つまるところは、微分をたくさん使いますというところです。別個に学習が必要かもしれない。。。
そして細かい計算は計算機を使用するようです。それならば、プログラムで計算したほうがより複雑で難解な計算でも行うことができます。
モデリング
モデリングの手法は大まかに2種類
- 理解志向型モデリング:データがどのようなメカニズムで生成されているか理解する、以下のような形にする
- 変数やパラメータの数を最小限にする
- 数理構造に使用する関数をできるだけ簡単にする
- 応用志向型モデリング:手元のデータをもとに、道のデータに対して予測・制御を行ったり、データの生成、利用を行う
- 数理モデルから出てくるデータを使う。用途としては「予測」と「生成」
- 画像解析(手書きの文字識別など)
次は「少数の方程式によるモデル」を学習します。(2021/02/21)
とりあえずはここまでです。
でわでわ。。。
数理モデル関連
第二弾
- 数学への挑戦 第二弾〜数理モデルxプログラミング〜
- 数学への挑戦 第二弾〜実装編:数理モデルxプログラミング〜
- 数学への挑戦 第二弾〜集合を使う:数理モデルxプログラミング〜
- 数学への挑戦 第二弾〜確率変数:数理モデルxプログラミング〜
- 数学への挑戦 第二弾〜期待値と分散:数理モデルxプログラミング〜
- 数学への挑戦 第二弾〜卒業までに彼氏ができる確率:数理モデルxプログラミング〜
- 数学への挑戦 第二弾〜確率変数の足し算:数理モデルxプログラミング〜
- 数学への挑戦 第二弾〜まとめ1:数理モデルxプログラミング〜

![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/18ff7e3e.9e81c26d.18ff7e3f.8be5cf26/?me_id=1213310&item_id=19973054&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F2494%2F9784802612494.jpg%3F_ex%3D400x400&s=400x400&t=picttext)


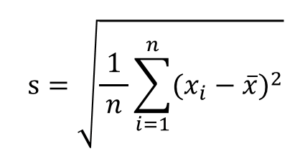


![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/18ff7e3e.9e81c26d.18ff7e3f.8be5cf26/?me_id=1213310&item_id=19335896&m=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F5687%2F9784860645687.jpg%3F_ex%3D80x80&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F5687%2F9784860645687.jpg%3F_ex%3D240x240&s=240x240&t=picttext)
 1(実現値) x 1/6(確率)
1(実現値) x 1/6(確率)